Rainfall Runoff Modelling Using Neural Networks Stateoftheart and Future Research Needs

Preparation of Artificial Neural Networks Using Information-Rich Data
1
National Institute of H2o and Atmospheric Research, Christchurch 8011, New Zealand
ii
National Plant of Hydrology, Roorkee 247667, India
three
Plant for Modelling Hydraulic and Environmental Systems, University of Stuttgart, 70569 Stuttgart, Frg
*
Writer to whom correspondence should exist addressed.
Received: 6 June 2014 / Revised: ix July 2014 / Accepted: 14 July 2014 / Published: 22 July 2014
Abstract
Artificial Neural Networks (ANNs) are classified as a data-driven technique, which implies that their learning improves as more and more grooming information are presented. This observation is based on the premise that a longer fourth dimension series of training samples will contain more events of different types, and hence, the generalization ability of the ANN will amend. However, a longer fourth dimension serial need not necessarily contain more information. If in that location is considerable repetition of the same type of information, the ANN may not become "wiser", and 1 may exist just wasting computational try and time. This study assumes that in that location are segments in a long time serial that contain a big breakthrough of information. The reason behind this supposition is that the information contained in any hydrological serial is not uniformly distributed, and it may be cyclic in nature. If an ANN is trained using these segments rather than the whole serial, the training would be the same or better based on the information contained in the series. A pre-processing tin be used to select information-rich data for grooming. However, almost of the conventional pre-processing methods do not perform well due to big variation in magnitude, scale and many zeros in the data series. Therefore, it is not very piece of cake to identify these information-rich segments in long fourth dimension series with big variation in magnitude and many zeros. In this report, the data depth function was used as a tool for the identification of critical (information) segments in a fourth dimension series, which does not depend on big variation in magnitude, scale or the presence of many zeros in data. Information from 2 gauging sites were used to compare the functioning of ANN trained on the whole information fix and simply the data from critical events. Pick of data for disquisitional events was washed by two methods, using the depth part (identification of critical events (ICE) algorithm) and using random selection. Inter-comparison of the performance of the ANNs trained using the complete information sets and the pruned data sets shows that the ANN trained using the data from critical events, i.due east., data-rich data (whose length could be 1 third to half of the series), gave similar results every bit the ANN trained using the complete data set up. However, if the data fix is pruned randomly, the performance of the ANN degrades significantly. The concept of this paper may be very useful for training data-driven models where the training time series is incomplete.
1. Introduction
As the proper name suggests, data-driven models (DDMs) attempt to infer the behaviour of a given system from the data presented for model grooming. Hence, the input data used for preparation should cover the unabridged range of inputs that the organisation is likely to experience, and the data of all the relevant variables should be used. Some modellers [1,ii,3,four,five] feel that the DDMs take the ability to determine which model inputs are critical, and then, a large amount of input information is given to the models, at times without whatever pre-processing. This approach has many disadvantages: more fourth dimension and effort is needed to train the model, and frequently, one may cease upwards at a locally optimal solution [vi]. Hence, the quality of data used for the training directly effects the accuracy of the model [7].
A number of studies have been carried out in the past to determine the inputs to the data-driven models [2,three,iv,vi,8,9,10]. In information-driven modelling (using, for example, techniques, such as a fuzzy, artificial neural network (ANN)), no rigorous criteria exist for input pick [eight]. Ordinarily used methods involve taking a time series model to decide the inputs for a DDM. A review of relevant studies was provided by [i,xi,12], where all of the authors accept pointed out that certain aspects of DDMs need to carry out extensive research; they are, namely, input choice, data sectionalization for training and testing, DDM grooming and extrapolation beyond the range of preparation data. Forecasting performance by DDMs is generally considered to be dependent on the data length [thirteen]. Hence, regarding the length of the information series, a common assumption is that the use of a longer fourth dimension serial of data will result in better training. This is because a longer series may contain unlike kinds of events, and this may better the training of DDMs. All the same, experience shows that a longer time serial does non necessarily mean more than information, because at that place can exist many repetitions of a similar blazon of information [14]. In such cases, one may non necessarily get a improve trained model, despite spending big computational time, and may over-fit the series [8,10]. In a review paper on the present state-of-art approaches to ANN rainfall-runoff (R-R) modeling by Jain et al. [11], at that place is the strong recommendation that there is a stiff need to deport out extensive research on different aspects while developing ANN R-R models. These include input selection, data division, ANN preparation, hybrid modelling and extrapolation beyond the range of training data. These research areas also employ to any DDMs. In a study, Chau et al. [15] employed 2 hybrid model, a genetic algorithm based on ANN and an adaptive network based on a fuzzy arrangement for overflowing forecasting for the Yangtze River in China. They found both models to be suitable for the chore, but they noted a limitation being the large number of parameters in an adaptive network based on a fuzzy organisation and large computational time in the genetic algorithm based on ANN.
From the above discussion, it can be concluded that the training of DDMs could be improved if the data of the events that are "rich" in information were used. Here, the term "rich" denotes the data with very high information content. Use of this term is based on the fact that some data epochs incorporate more information about the system than others. Bachelor input data tin be pre-processed to get out out the data that does non contain any new data. This is important in preparation a DDM, because these critical events mainly influence the training process and the calculation of weights.
In that location are several information pre-processing techniques, for example moving average, singular spectrum analysis, wavelet multi-resolution analysis, factor assay, etc. These techniques were coupled with an artificial neural network to improve the prediction by bogus neural network models [xvi,17,18,19]. In a study, Wu et al. [18] found that the pre-processing of data performed meliorate than a model fed by original data in a data-driven model. Chen and Chau [xx] implement a prototype cognition-based system for model manipulation for hydrological processes by employing an expert system beat out. Wu et al. [21] proposed a distributed support vector regression for river stage prediction. They found that distributed support vector regression performed better than the ANN, liner regression or nearest-neighbour methods. In a study, Wang et al. [22] employed ensemble empirical model decomposition for decomposing almanac rainfall serial in a R-R model based on support vector machine and applied particle swarm optimization to decide the gratis parameters of the support vector machine. They found that annual runoff forecast was improved using the particle swarm optimizing method based on empirical model decomposition. Jothiprakash and Kote [23] used information pre-processing for modelling daily reservoir inflow using a data-driven technique, and they found that intermittent inflow during the monsoon period lone could exist modelled well, using the full yr data, merely model prediction accuracy increases when only the seasonal information set for the monsoon menstruation is used. This but implies that the information content in a series plays a big role in the model training, hence the prediction accuracy. In a written report, Moody and Darken [24] trained networks in a completely supervised mode using local representations and hybrid learning rules. They institute that the networks learn faster than back propagation for 2 reasons, namely: the local representations ensure that only a few units respond to whatever given input that reduces the computational overhead; and the hybrid learning rules are linear, rather than nonlinear, thus leading to faster convergence. An overview of data preprocessing focusing on the problems of existent-world data can be establish in [25]. Data pre-processing is beneficial in many ways. One can eliminate irrelevant data to produce faster learning, due to smaller data sets and due to the reduction of defoliation caused by irrelevant information [25]. Most of the conventional pre-processing techniques, such as transformation and/or normalization of data, do not perform well, because of the large variation in magnitude and scale, as well as the presence of many zero values in data serial [23]. Data from the real world are never perfect; it can be an incomplete tape with missing information, occurrence of zeros, improper types, erroneous records, etc.; hence, information pre-processing can be an iterative and tedious task.
To overcome the to a higher place-mentioned problems in the conventional pre-processing of data for input grooming for whatever DDMs, in this report, the geometrical properties of data were used to identify critical events from the long time series of information. The identification of disquisitional events (ICE) algorithm developed past [26,27], which employs Tukey [28] a half-space depth function, was used to identify the disquisitional events from the data series. Information technology is not afflicted by large variation in magnitude, scale or the presence of many zero values in a series. The Water ice algorithm is successfully used to meliorate the calibration of a conceptual and a physically-based model [27,29]. In previous studies [26,27,29,xxx,31], the ICE algorithm was not used in the field of DDMs. Since DDMs depend more often than not on information and data independent on data series, the authors believe DDMs can benefit nigh from the Water ice algorithm. Hence, in this written report, an artificial neural network, which is a DDM approach, was trained on the disquisitional events identified by the ICE algorithm and compared with the training of ANN with randomly selected events, as well equally with the ANN trained on the whole data ready.
The purpose of this paper is to test the ICE algorithm and to improve the preparation efficiency of the information-driven model past using information-rich data. In this written report, the ANN approach was used to institute an integrated stage belch-sediment concentration relationship for two sites on the Mississippi River. The ANN model was trained firstly on the entire time series of available data; secondly, the ANN was trained on critical events selected past the ICE algorithm, and finally, the ANN was trained on randomly selected events. A comparison was made on these cases to ascertain the feasibility of training the ANN model on disquisitional events. The newspaper is organized as follows: following the Introduction, the methodology is presented in Section ii. In Department iii, a case study that attempts to train a sediment rating curve using ANN is described. In the concluding section, results are discussed and conclusions are drawn.
2. Methodology
The information contained in any hydrological series is not homogeneous [xiv]. The data that contain lots of hydrological variability may be the best choice for training, because they comprise most of the information for parameter (weights) identification [32]. In this study, the data with the about hydrological variability in a information series is termed every bit the critical events. To identify the critical events, the concept of the data depth function was used in this written report. This concept is briefly described beneath.
two.1. Data Depth Office
Data depth is cipher merely a quantitative measurement of how central a point is with respect to a data prepare or a distribution. A depth role was get-go introduced by [28] to identify the center (a kind of generalized median) of a multivariate data set. Several generalizations of this concept accept been defined in [33,34,35]. Several types of data depth functions accept been developed. For example, the half-space depth function, the L1 depth function, the Mahalanobis depth function, the Oja median, the convex hull peeling depth function and the simplicial median. For more detailed information about the data depth function and its uses, please refer to [thirty,33] and [36]. The methodology presented in this study is not afflicted by the choice of the data depth function. Tukey's half-space depth is one of the about popular depth functions bachelor, and information technology is conceptually unproblematic and satisfies several desirable properties of depth functions [37]. Hence, in this study, the half-space data depth function was used.
The half-space depth of a signal pwith respect to the finite set X in the d dimensional infinite is defined as the minimum number of points of the set X lying on ane side of a hyperplane through the point p. The minimum is calculated over all possible hyperplanes. Formally, the half-space depth of the point p with respect to set 10 is:
Here, (x, y) is the scalar production of the d dimensional vectors and
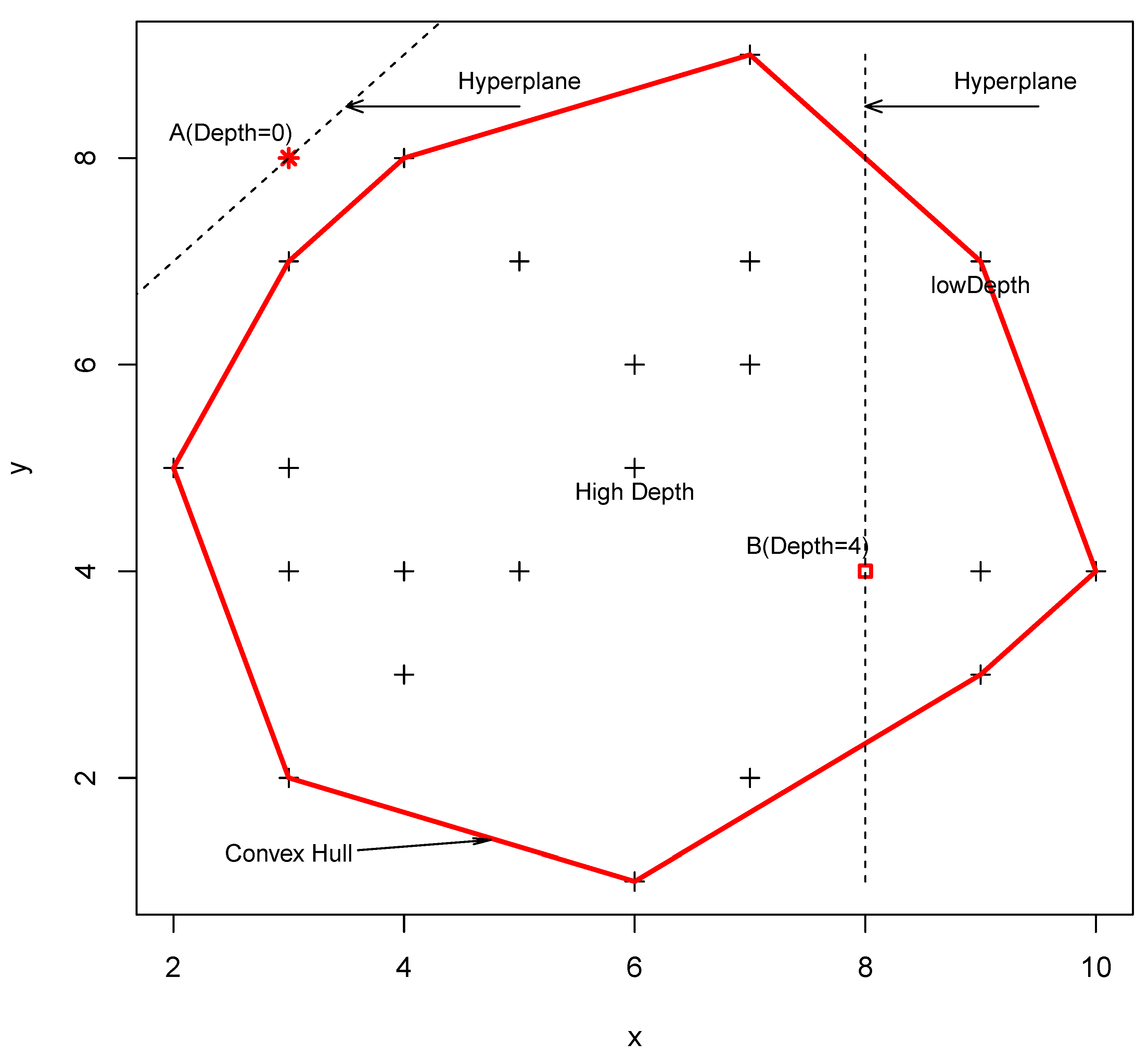
is an arbitrary unit vector in the d dimensional space representing the normal vector of a selected hyperplane. If the point p is exterior the convex hull of X, then its depth is 0. The convex hull of a set of points S is the smallest area polygon which encloses Due south. A formal instance of convex hull is given in Figure 1. Points on and near the purlieus accept low depth, while points deep inside have a loftier depth. One advantage of this depth role is that it is invariant to affine transformations of the space. This means that the unlike ranges of the variable accept no influence on their depth. The notion of the information depth function is not oftentimes used in the field of water resources. Chebana and Ouarda [36] used depth to identify the weights of a non-linear regression for flood estimation. Bárdossy and Singh [30] used the data depth function for parameter interpretation of a hydrological model. Singh and Bárdossy [27] used the data depth function for the identification of disquisitional events and developed the ICE algorithm. Recently, Singh et al. [31] used the data depth part for defining predictive uncertainty.
Figure 1. Example of a convex hull.
Effigy 1. Example of a convex hull.
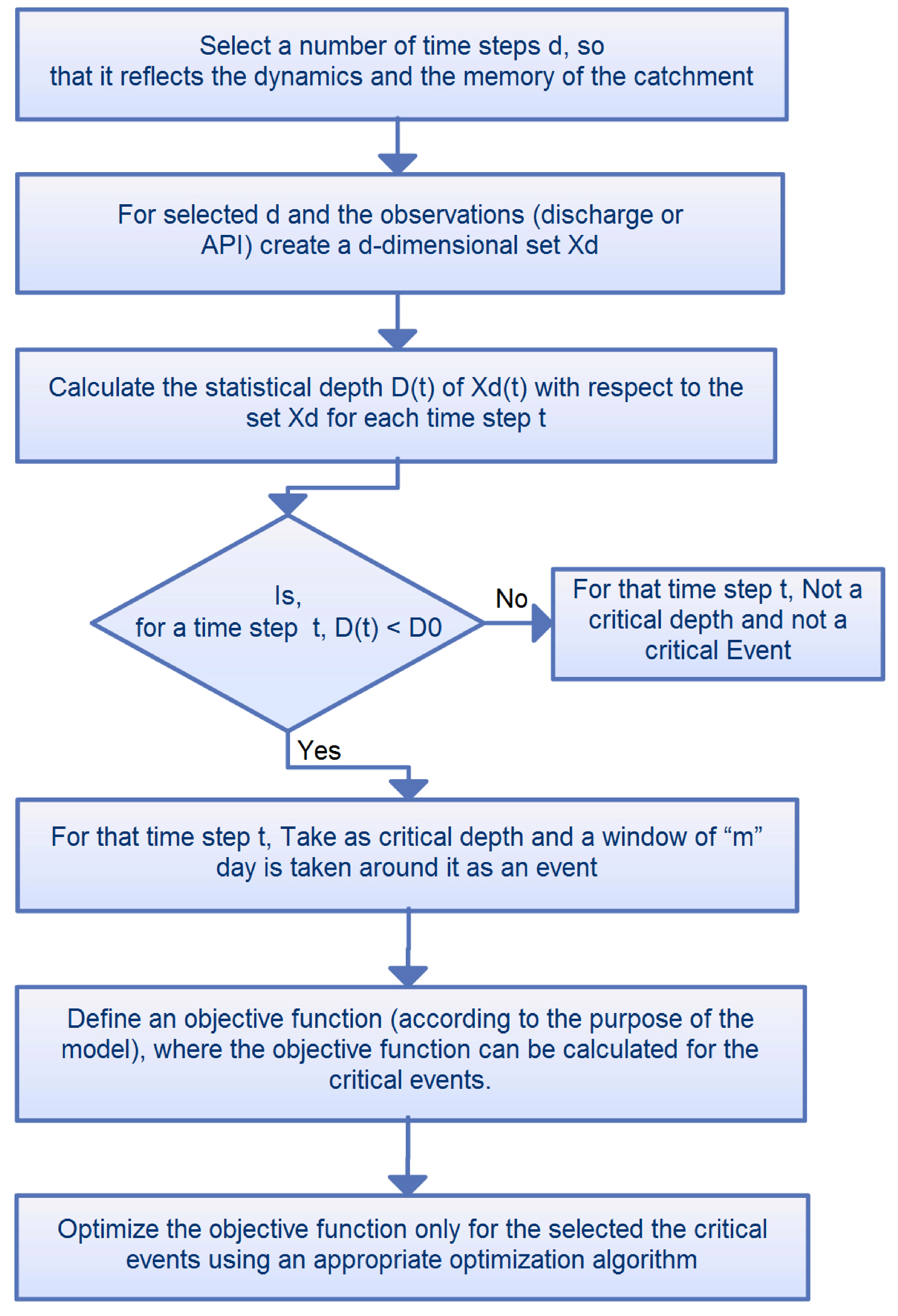
Effigy 2. Flow chart for the identification of critical events (Water ice) algorithm [29].
Figure ii. Flow chart for the identification of critical events (Ice) algorithm [29].
2.2. Identification of Critical Time Period Using the Data Depth Office
The information content of the data can significantly influence the training of a information-driven model. Hence, if we tin select just those data that are hydrologically reliable and are from a critical time menstruation that has more variability, then we may improve our grooming process [32]. The Ice algorithm for the identification of critical events adult by [27] was used in this study. A flow chart for the ICE algorithm is given in Figure two, where the instance of result option using belch or the Antecedent Precipitation Index (
) is described. A brief description of the algorithm is given here. For details, please refer to [26,27]. To place the critical time menstruation that may contain enough data for identifying the model weights, unusual sequences in the serial have to exist identified. For simplicity, denote
for a given stage, discharge and sediment. For each t, the statistical depth
with respect to the set
is calculated and denoted by
. The statistical depth is invariant to affine transformations. Depth tin can be calculated from untransformed observation series of stage, belch and sediment. Time steps t with a depth less than the threshold depth (
) are considered to exist unusual. This is simply because unusual combinations in the multivariate instance will cause a low depth. In practise, a more variable fourth dimension period will have low depth, and it is useful for the identification of model weights. Such a set
for
, calculated from the daily discharges, and the points with low depth are on the boundary of the convex hull, as shown in Figure 1. All of the points inside the convex hull have a higher depth. In this newspaper, critical events are defined around the unusual (low depth) days. A time t is part of a critical event if there is an unusual time
in its neighbourhood defined as
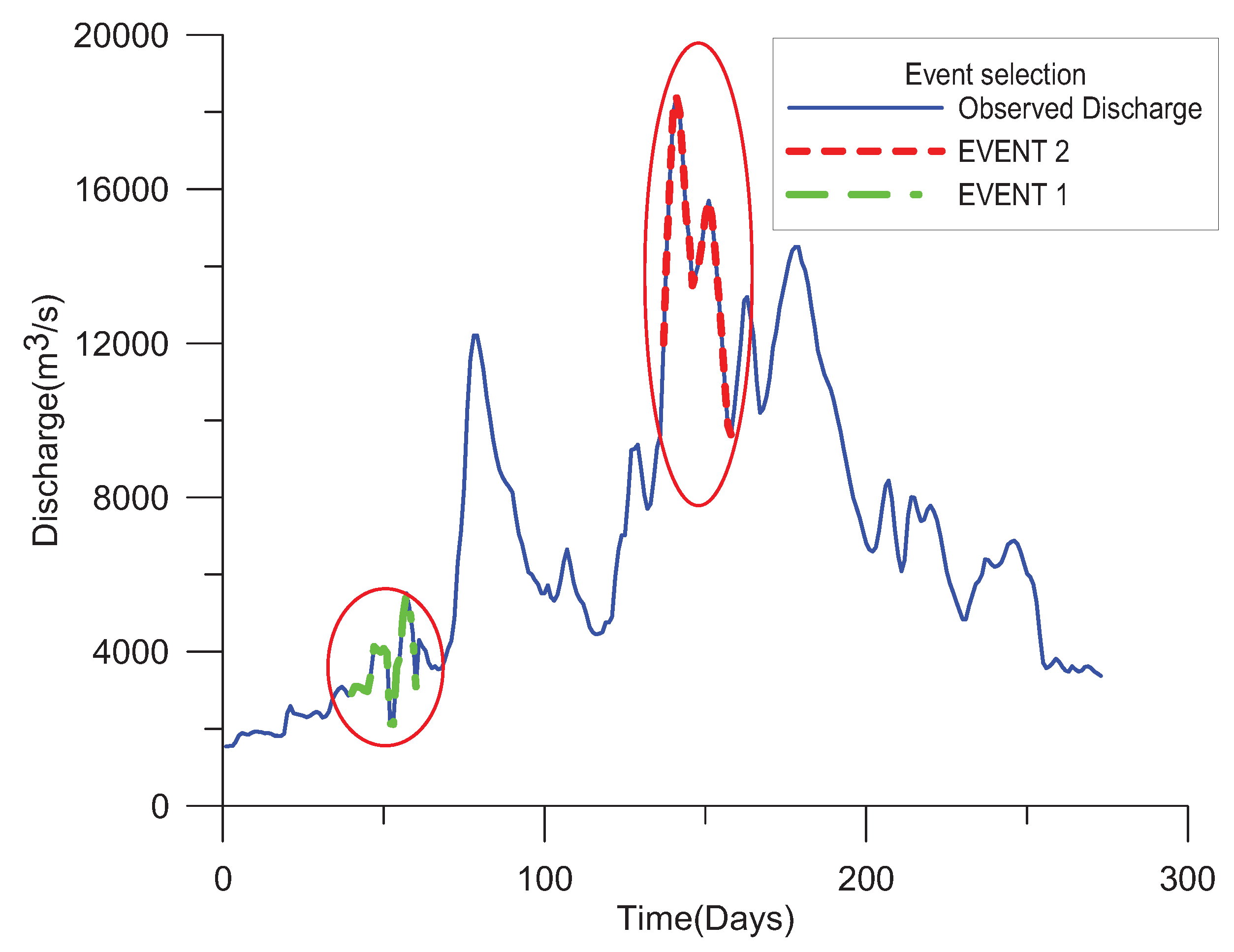
. An case of events selected by using stage, discharge and sediment is given in Figure 3. Please note that the critical events are not only the extreme values in the series; instead, it is the combination of depression menstruum, high flow, etc.
Figure 3. Example of event selection.
Figure 3. Instance of event selection.
iii. Case Report
The methodology presented in the last section volition be demonstrated using ANN to construct a sediment rating curve. For the design and management of a water resource projection, it is very much essential to know the volume of sediments transported by a river. It is possible to directly measure out how much sediment is transported by the river, but not continuously. Consequently, a sediment rating curve is generally used. These curves can be synthetic past several methods. In this regard, ANNs seem to exist viable tools for fitting the relationship between river discharge and sediment concentration.
iii.ane. Bogus Neural Networks
Artificial neural networks derive their key theme from highly simplified mathematical models of biological neural networks. ANNs have the ability to learn and generalize from examples to produce meaningful solutions to problems, even when the input data contains errors or is incomplete. They tin also process information quickly. ANNs are capable of adapting their complexity to model systems that are non-linear and multi-variate and whose variables involve circuitous inter-relationships. Furthermore, ANNs are capable of extracting the relation between the input and output of a process without any noesis of the underlying principles. Because of the generalizing capabilities of the activation office, i need not make any supposition most the relationship (i.e., linear or not-linear) betwixt input and output.
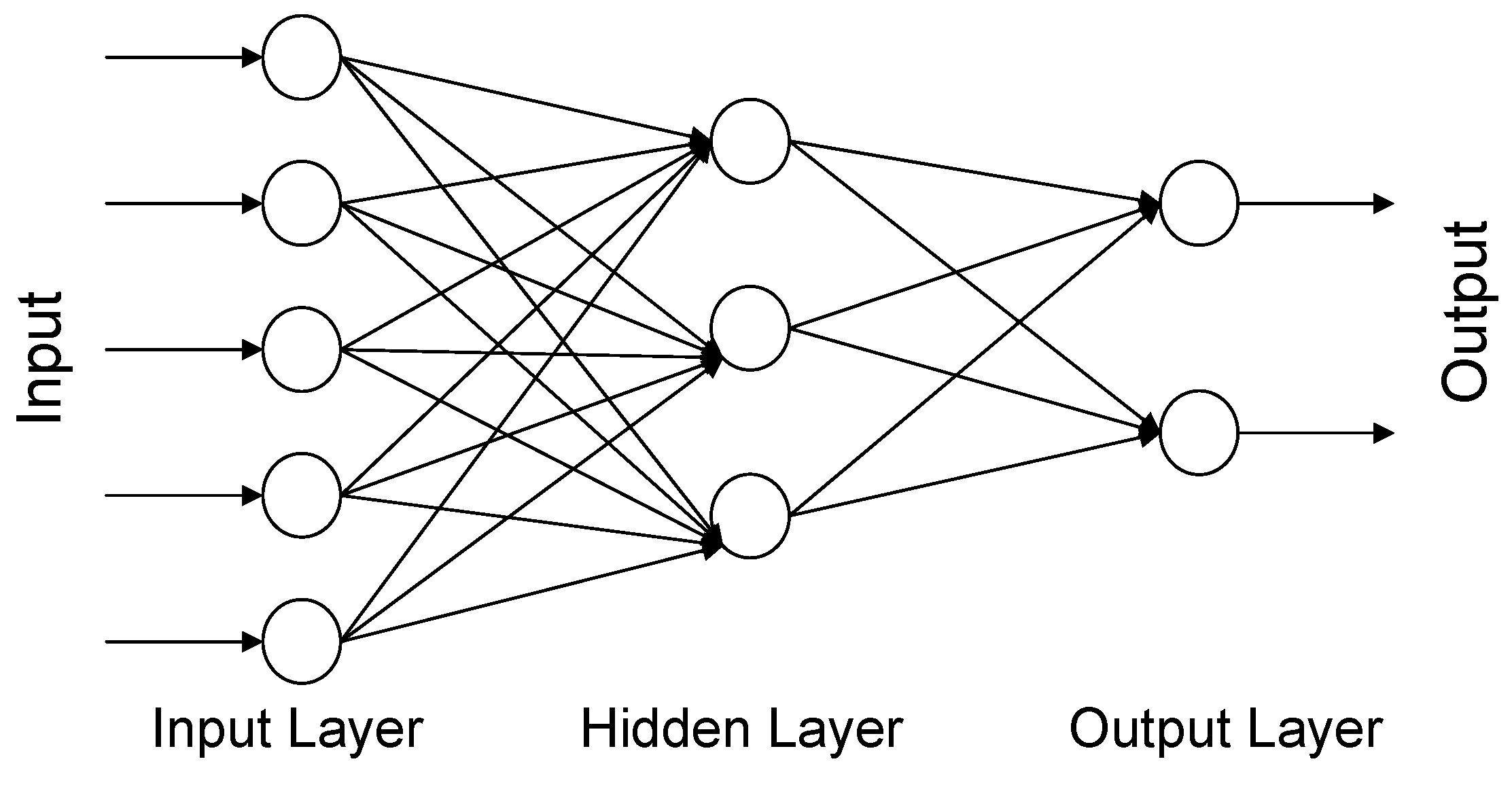
Since the theory of ANNs has been described in numerous papers and books, the aforementioned is described here in brief. A typical ANN consists of a number of layers and neurons; the most unremarkably used neural network in hydrology existence a 3-layered feed-forward network. The menstruation of data in this network takes place from the input layer to the hidden layer and so to the output layer.
The input layer is the first layer of the network, whose role is to pass the input variables onto the next layer of the network. The terminal layer gives the output of the network and is appropriately called the output layer. The layer(s) in between the input and output layer are chosen hidden layer(s). The processing elements in each layer are called neurons or nodes. The numbers of nodes in input and output layers depends on the problem to be addressed and are decided before commencing the training. The number of hidden layers and the number of nodes in each subconscious layer depend on the problem and the input data and are commonly adamant past a trial and fault procedure. A synaptic weight is assigned to each link to correspond the relative connection strength of ii nodes at both ends in predicting the input-output relationship. The output of any node j,
, is given every bit:
where
is the input received at node j,
is the input connection pathway weights, m is the full numbers of inputs to node j and
is the node threshold. Function f is an activation office that determines the response of a node to the total input indicate that is received. A sigmoid function is the unremarkably used activation office, which is bounded above and below, is monotonically increasing and is continuous and differentiable everywhere.
The error back propagation algorithm is the most popular algorithm used for the grooming of feed-forward ANNs [38]. In this process, each input pattern of the preparation data set is passed through the network from the input layer to the output layer. The network output is compared with the desired target output, and an error is computed equally:
where
is a component of the desired output T,
is the respective ANN output, p is the number of output nodes and P is the number of preparation patterns. This error is propagated backward through the network to each node, and correspondingly, the connection weights are adapted.
Due to the boundation of the sigmoid function between goose egg and ane, all input values should be normalized to fall in the range betwixt cypher and one before being fed into a neural network [39]. The output from the ANN should exist denormalized to the original domain before interpreting the results. ASCE [38,40] contains a detailed review of the theory and applications of ANNs in h2o resource. Maier and Dandy [1] have also reviewed modeling issues and applications of ANNs for the prediction and forecasting of hydrological variables. Maier et al. [41] have provided a state-of-the-art review of ANN applications to river systems.
Govindaraju and Rao [42] have described many applications of ANNs to water resources. ANNs accept been applied in the expanse of hydrology, including rainfall-runoff modeling [43,44,45], river stage forecasting [46,47,48,49], reservoir operation [50], describing soil h2o retention curves [51] and optimization or control issues [52]. ANN was employed successfully for predicting and forecasting hourly groundwater level upwardly to some fourth dimension ahead [53]. In a report, Cheng et al. [54] developed various ANN models with various training algorithm to forecast daily to monthly river flow discharge in Manwar Reservoir. A comparison of ANN model with a conventional method, like automobile-regression, suggests that ANN provides improve accuracy in forecasting. Other studies have also shown that ANNs are more accurate than conventional methods in flow forecasting and drainage blueprint [55].
Furthermore, the ANN method was used extensively for the prediction of various variables (stream flow, atmospheric precipitation, suspended sediment, etc.) in the h2o resource field [17,43,51,56,57,58,59,sixty,61,62,63,64,65,66]. Kumar et al. [67] found that an ANN model can be trained to predict lysimeter potential evapotranspiration values better than the standard Penman–Monteith equation method. Sudheer et al. [68] and Keskin and Terzi [69] tried to compute pan evaporation using temperature data with the assist of ANN. Sudheer and Jain [seventy] employed a radial-basis part ANN to compute the daily values of evapotranspiration for rice crops. Trajkovic et al. [71] examined the functioning of radial basis neural networks in evapotranspiration estimation. Kisi [72] studied the modelling of evapotranspiration from climatic data using a neural computing technique, which was plant to be superior to the conventional empirical models, such as Penman and Hargreaves. Modelling of evapotranspiration with the assistance of ANN was also attempted by Kisi [73], Kisi and Öztürk [74] and Jain et al. [75]. Muttil and Chau [76] used ANN to model algal bloom dynamics. ANN has besides been used in h2o quality modeling [77,78,79].
3.2. Data Used in the Study
The data used in this study was the same as used by [eighty]. For more details about the study area and data, please refer to [80]. Sufficiently long time series to obtain stable parameters from two gauging stations on the Mississippi River were available. Both stations are in Illinois and operated by the U.South. Geological Survey (USGS). These stations are located virtually Chester (USGS Station No. 07020500) and Thebes (USGS Station No. 07022000). The drainage areas at these sites are one,835,276 km
(708,600 mi
) for Chester and 1,847,190 km
(713,200 mi
) at Thebes. For these stations, daily fourth dimension series of river belch and sediment concentration were downloaded from the spider web server of the USGS, and the river phase information were provided by USGS personnel. River belch and sediment concentration were continuously measured at these sites for estimating the suspended-sediment belch. For more than details nigh the sites, the measurement procedures, etc., please refer to [81] and [82]. After examining the data and noting the periods in which there were gaps in one or more of the three variables, the periods for training and testing were chosen. For the Chester station, the data of 25 December 1985, to 31 August 1986, were chosen for training, and the data from 1 September 1986, to 31 January 1987, were chosen for testing. For the Thebes station, the data from ane January 1990, to thirty September 1990, were used for grooming, and data from 15 Jan 1991, to x August 1991, were used for testing. It may be noted that the periods from which grooming and testing data were chosen for the Thebes site span approximately the same temporal seasons (January–September and January–August). The information for the Chester site, nonetheless, covers slightly dissimilar months (i.e., Dec–Baronial and September–Jan). Based on our feel on the employ of very long time serial or unlike time steps for the information, the results of the study are non expected to modify.
3.3. Rating Curves and Input to ANN
The records of stage tin can be transferred into records of belch using a rating curve. Ordinarily, a rating curve has the class:
where Q is belch (m
/s), H is river stage (thousand) and a and b are abiding. The establishment of a rating curve is a non-linear problem. In a study, Jain and Chalisgaonkar [83] showed that ANN can correspond the stage and discharge relation better than the conventional fashion, which uses Equation (iv).
A sediment rating bend has a very similar non-linear form as a discharge rating curve. Unremarkably, the relationship is given by:
where S is the suspended sediment concentration (mg/L), Q is discharge (m
/s) and c and d are constant. Please note that establishing a sediment rating curve is a two-step process. The measured stage data are used to estimate discharge, and then, discharge is used to establish the sediment rating curve. Therefore, river stage, discharge and sediment concentration are the chief inputs for analysis.
The inputs to the ANN were river stages at the current and previous times. The other inputs were water belch and sediment concentration at previous times. The input to the ANN model was standardized before applying ANN. The input was normalized by dividing the value with the maximum value to fall in the range [0, 1]. This ANN had two output nodes, one respective to water discharge and the other for sediment concentration. In a study, Jain [80] tried various combinations of input data of the phase, discharge and sediment concentration for the ANN model and constitute that the number of neurons in the hidden layer varies between two to x. They suggest a network whose inputs are the current and previous stage; the discharge and sediment concentration of 2 previous periods can adequately map the current discharge and sediment concentration. Since the aim of this study was to test the feasibility of training the ANN model on disquisitional events, we used the same setup of network as given by [eighty]. Hence, an integrated 3-layer ANN, as described by Jain [80], was trained using the grooming period data pertaining to river phase, discharge and sediment concentration (Effigy four). The number of nodes in the hidden layer was determined based on the best correlation coefficient (CC) and the to the lowest degree root mean foursquare (RMSE). Using the weights obtained in the training phase for each case, the performance of the ANN was checked by using the testing period data.
Programs were adult in MATLAB vi.five software using the neural network toolbox to pre-process the information, railroad train the ANN and test it. The weights were obtained past the Levenberg–Marquardt algorithm, which is computationally efficient.
Effigy iv. Three-layer, feed-forward ANN construction.
Figure 4. Three-layer, feed-forward ANN construction.
three.iv. Different Cases for the Training of ANN
To compare the training results of the ANN model on disquisitional events with training on the whole data serial, for each data set, the ANN model was trained and tested for iii cases. The three different cases are given below.
-
Example ane: using the entire fourth dimension series of data available,
-
Case 2: using the data pertaining to disquisitional events but (selected by the depth function (ICE algorithm)), and
-
Example 3: using the data pertaining to randomly selected events (the same number of events as in Case ii). Here, a number of runs were taken by randomly selecting the events, and the results reflect the average of ten repetitions.
4. Results and Discussion
Stage, discharge and sediment rating relations were adamant for both sites using the ANN by following the same procedure as used by [80]. For both, the site river stage and discharge relationship was fitted using Equation (iv); then, respective sediment discharge was computed using Equation (five). The ANN model was trained and tested on three different cases described in Section three.5. RMSE and CC were used to test the results of the model in training and testing. RMSE accounts for the magnitude of the disagreement between the model and what is observed, whereas CC accounts for the disagreement in the dynamics of the model and what is observed. Table 1 and Table two give the RMSE and correlation between the observed and the model for each case for the Chester site for the training and testing menses, respectively. It can be seen from Tabular array one that for discharge, the CC and RMSE are virtually the aforementioned for Cases i and two; CC and RMSE for Case 3 are somewhat inferior. For the sediment concentration information, CC and RMSE were slightly inferior for Case 3. Testing results given in Table 2 prove that for the belch data, CC is very high and is nearly the same for Cases 1 and 2, whereas information technology is a "bit smaller" for Instance iii; the RMSE is bit higher for Case 3. For the sediment data, CC is very high for Instance two and is lower and nigh the aforementioned for Case 1 and 3; the RMSE is the all-time for Example 2, followed by Instance ane, and worst for Case 3. In both the training and testing period, Case three has shown poor operation, equally compared to Case i and 2 in terms of RMSE and CC. This shows that the random selection of events for training is non suitable for training ANN models. This is simply considering the random selection of an event does non represent the entire series, whereas critical events correspond the whole series.
Table 1. The RMSE and correlation coefficient for the ANN model for the training period for the Chester site.
| Cases | Discharge | Sediments | % | ||
|---|---|---|---|---|---|
| Correlation | RMSE | Correlation | RMSE | Data Used | |
| Case i | ix.977×10 | ane.330×x | ix.537×x | 6.116×10 | 100 |
| Case two | 9.979×ten | one.503×10 | nine.502×ten | seven.823×10 | 53 |
| Example iii | 9.954×10 | 2.309×10 | 9.212×10 | 7.908×ten | 53 |
Table 2. The RMSE and correlation coefficient for the ANN model for the testing menstruum for the Chester site.
| Cases | Discharge | Sediments | ||
|---|---|---|---|---|
| Correlation | RMSE | Correlation | RMSE | |
| Case 1 | 9.928×10 | 6.557×10 | eight.695×10 | 7.874×10 |
| Instance two | 9.904×10 | 6.914×x | 9.049×10 | 6.859×ten |
| Case 3 | 9.670×ten | 2.129×10 | eight.444×10 | 1.225×10 |
To help the visual appraisal of the results, time serial graphs were prepared. Figure five presents the observed and computed belch for various cases for the Chester station for the testing menstruum. The match is very expert, except for the start and the major pinnacle. Overall, the match is the best for Instance 1 followed past Case 2 and Case 3, the deviation between Example one and 2 existence modest. Figure 6 presents the fourth dimension series plot for the sediment data. Here, for some peaks and troughs, the graph for Example 1 is closer to what is observed, while for some others, the graph for Case ii is closer. The graph for Case 3 appears to be consistently under performing. The time series plots for belch and sediments for the ANN model based on Case 3 is inferior, both in timing, as well as in magnitude. Hence, it fails to correspond the magnitude and dynamics of the series. These outcome are coming from the use of randomly selected events, which may not have enough information for training the model. These figures affirm the interpretation of the results from Table one and Table 2, that the ANN estimates by using the whole data and the ANN trained on critical events testify a nearly similar match with the observed bend, whereas grooming past the random selection of events is inferior.
Table three and Table 4 requite the RMSE and CC for the three cases for the Thebes site for the training and testing period, respectively. Results in Table 3 show that for discharge, the CC is very high and nearly the same for Cases i and 2, while information technology is a bit smaller for Case three. The same tin can be said for RMSE, which is almost twice for Instance 3 compared to Case ii. Both CC and RMSE are junior for Example iii. For sediment concentration data, CC is highest for Example ane, followed by Case ii and and so Example 3. The RMSE was very small for Case 1 and was almost the same for the remaining two cases.
Figure five. Observed and computed discharge for each example for the Chester site testing period.
Figure 5. Observed and computed discharge for each case for the Chester site testing period.
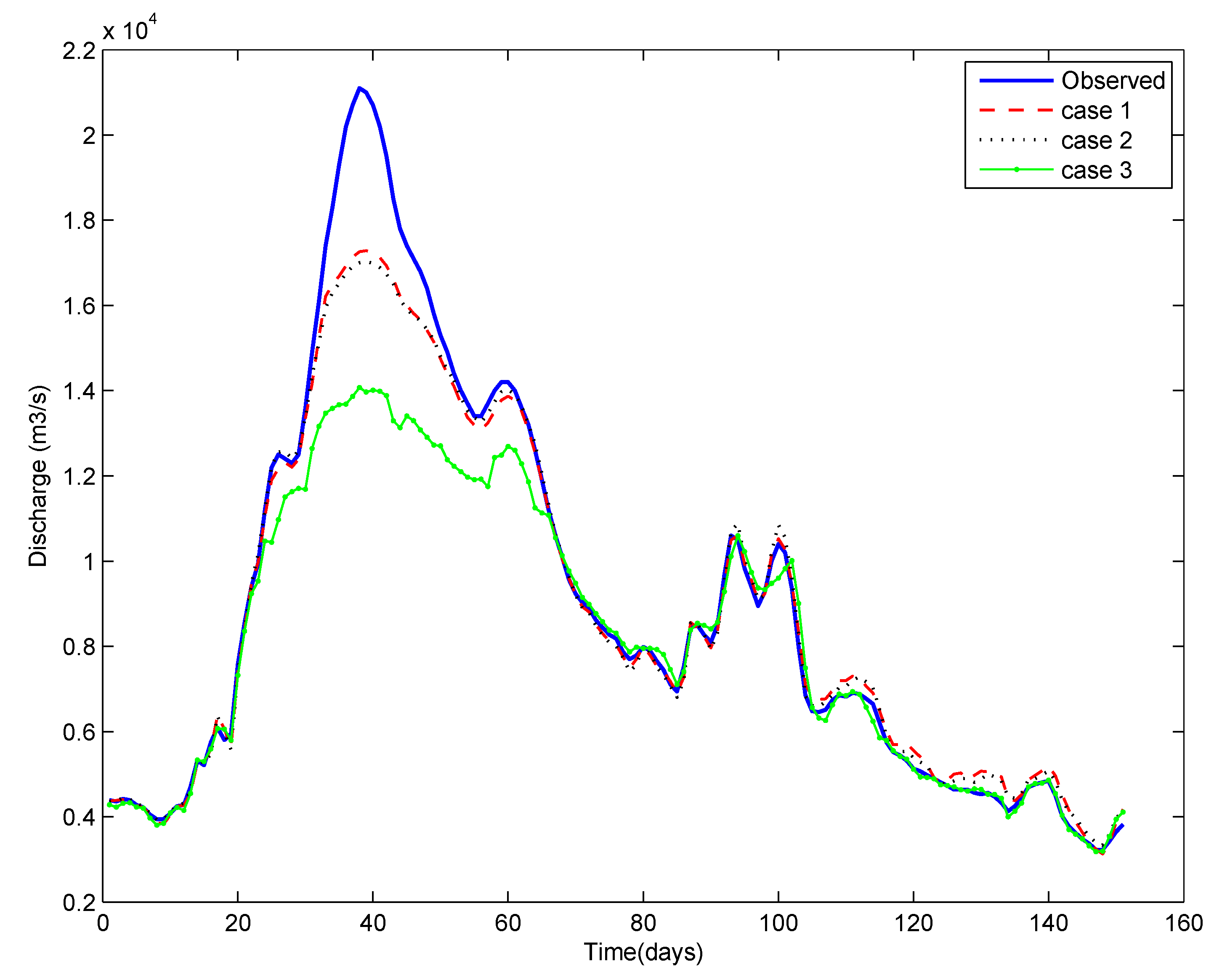
Figure half-dozen. Observed and computed sediment concentration for each case for the Chester site testing period.
Figure half dozen. Observed and computed sediment concentration for each case for the Chester site testing menstruum.
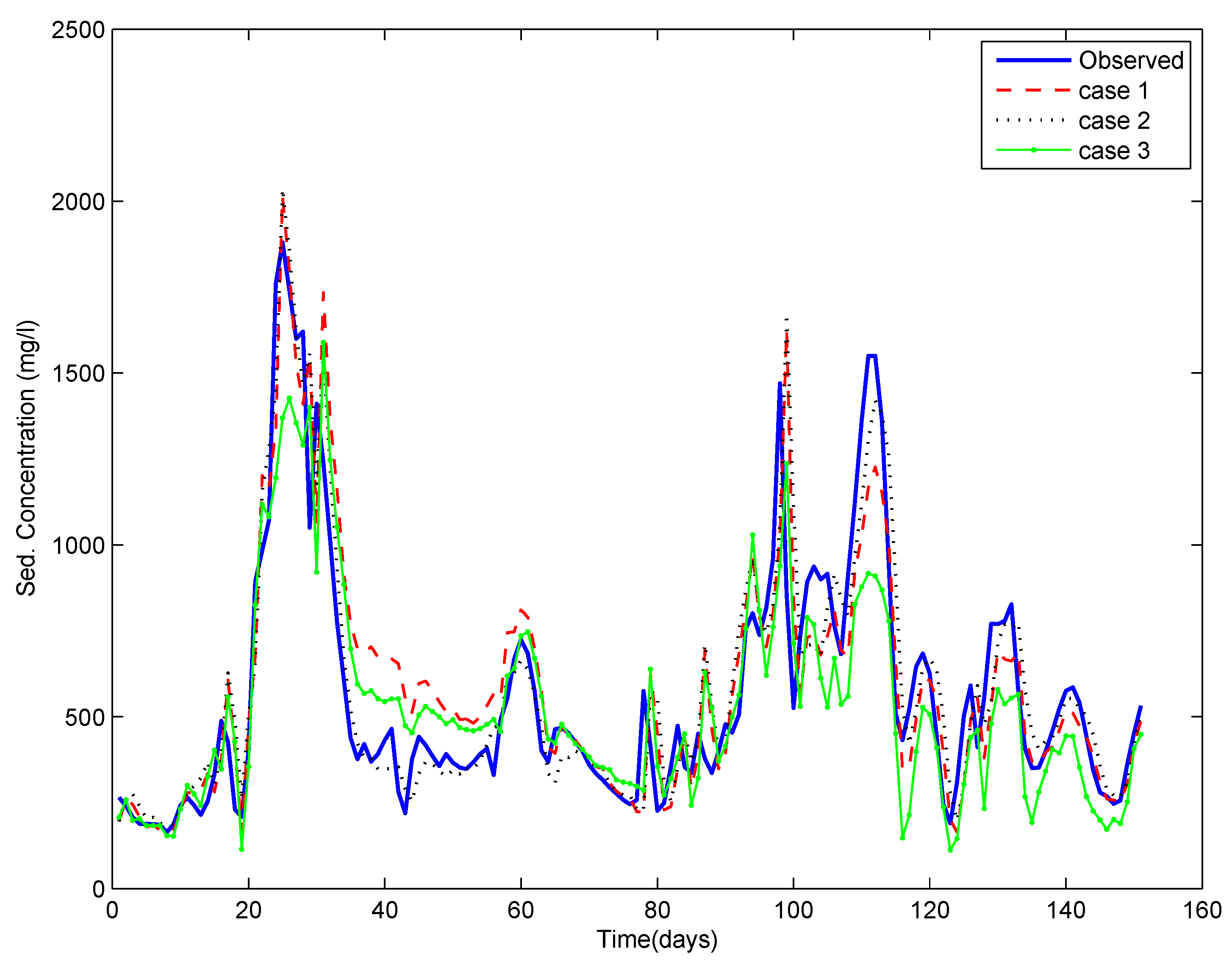
Testing results given in Table 4 show that for discharge, CC is very high and is nearly the same for Case i and 2; it was smaller for Case 3. The RMSE was quite high for Case 3, every bit compared to the other 2 cases. For the sediment data, the functioning indices had a similar behaviour: CC was much less, and the RMSE was much loftier for Case 3 compared to the other two cases.
Table 3. The RMSE and correlation coefficient for the ANN model for the training period for the Thebes site.
| Cases | Discharge | Sediments | % | ||
|---|---|---|---|---|---|
| Correlation | RMSE | Correlation | RMSE | Data Used | |
| Case 1 | 9.946e-01 | ii.137e-02 | 9.045e-01 | 5.636e-02 | 100 |
| Case 2 | 9.929e-01 | iii.273e-02 | eight.296e-01 | 1.023e-01 | 29 |
| Example 3 | nine.723e-01 | vi.034e-02 | vii.425e-01 | 9.816e-02 | 29 |
Table 4. The RMSE and correlation coefficient for the ANN model for the testing period for the Thebes site.
| Cases | Belch | Sediments | ||
|---|---|---|---|---|
| Correlation | RMSE | Correlation | RMSE | |
| Instance i | 9.975e-01 | one.085e-02 | 9.439e-01 | iii.987e-02 |
| Example ii | 9.949e-01 | ii.226e-02 | 9.440e-01 | 4.049e-02 |
| Case 3 | 9.273e-01 | ane.017e-01 | eight.984e-01 | 1.510e-01 |
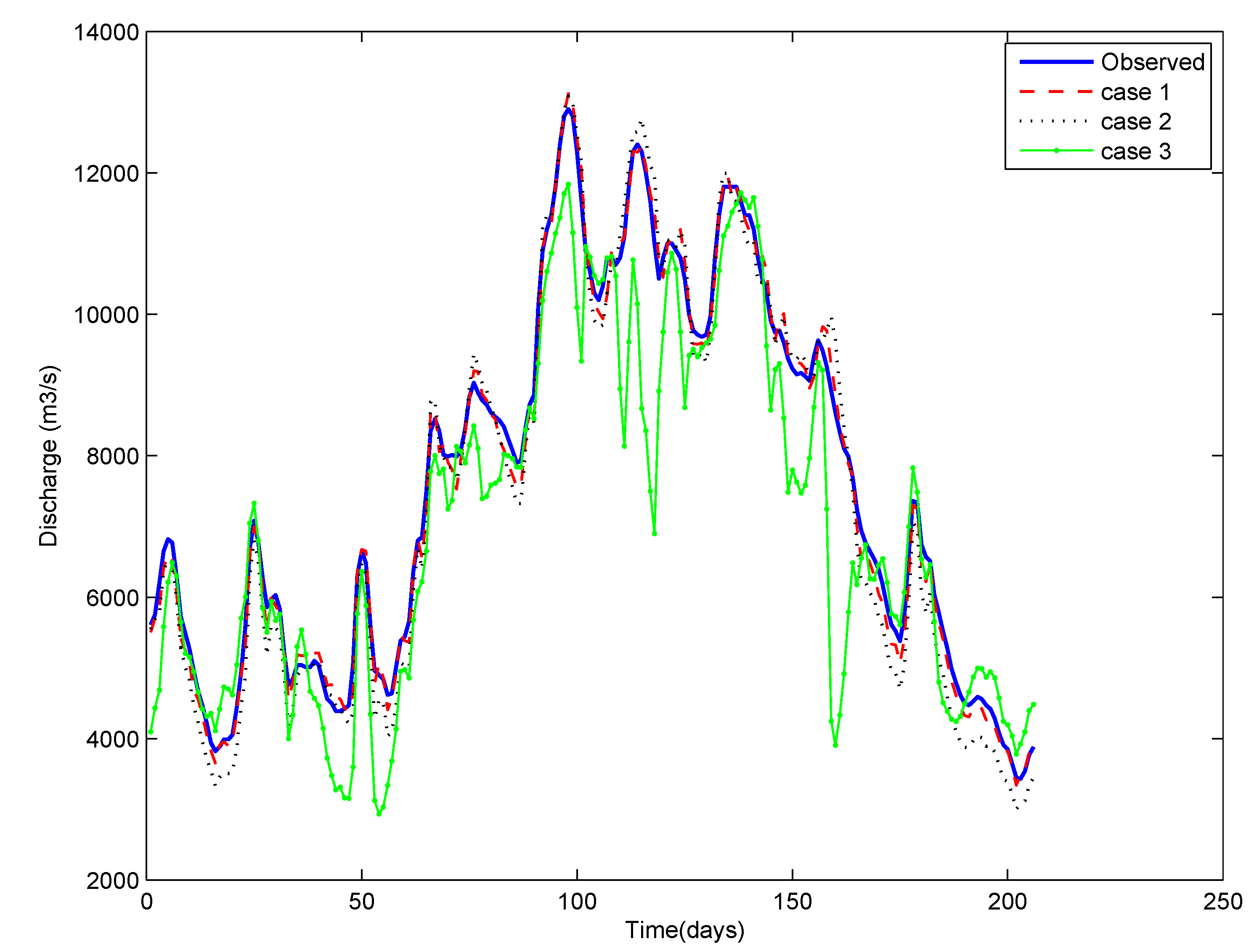
Figure 7 shows the temporal variation of observed discharge and the estimates for all of the to a higher place three cases using ANN for the preparation period for the Thebes site. It tin be appreciated from this figure that the graphs pertaining to Cases 1 and ii are very close to the observed discharge bend, whereas the data for random events has been unable to railroad train the ANN properly. A poorly-trained ANN fails in the examination runs, every bit evidenced in Effigy 8. These results are very like to what we obtained for the Chester site.
Figure 7. Observed and computed discharge for each case for the Thebes site testing flow.
Figure seven. Observed and computed belch for each case for the Thebes site testing period.
Based on these results, it can exist stated that the functioning of ANN grooming using "data-rich" events is as good as that using the whole information set. At first glance, this statement may appear to claiming the widely repeated concept that an ANN becomes wiser as more than data are used to train it. Nevertheless, upon closer scrutiny, this concept supports the fact that if the data has multiple events that contain similar information well-nigh the natural system, and then the ANN is non going to acquire much despite spending a long time in preparation.
Figure eight. Observed and computed sediment concentration for each case for the Thebes site testing flow.
Figure 8. Observed and computed sediment concentration for each instance for the Thebes site testing period.
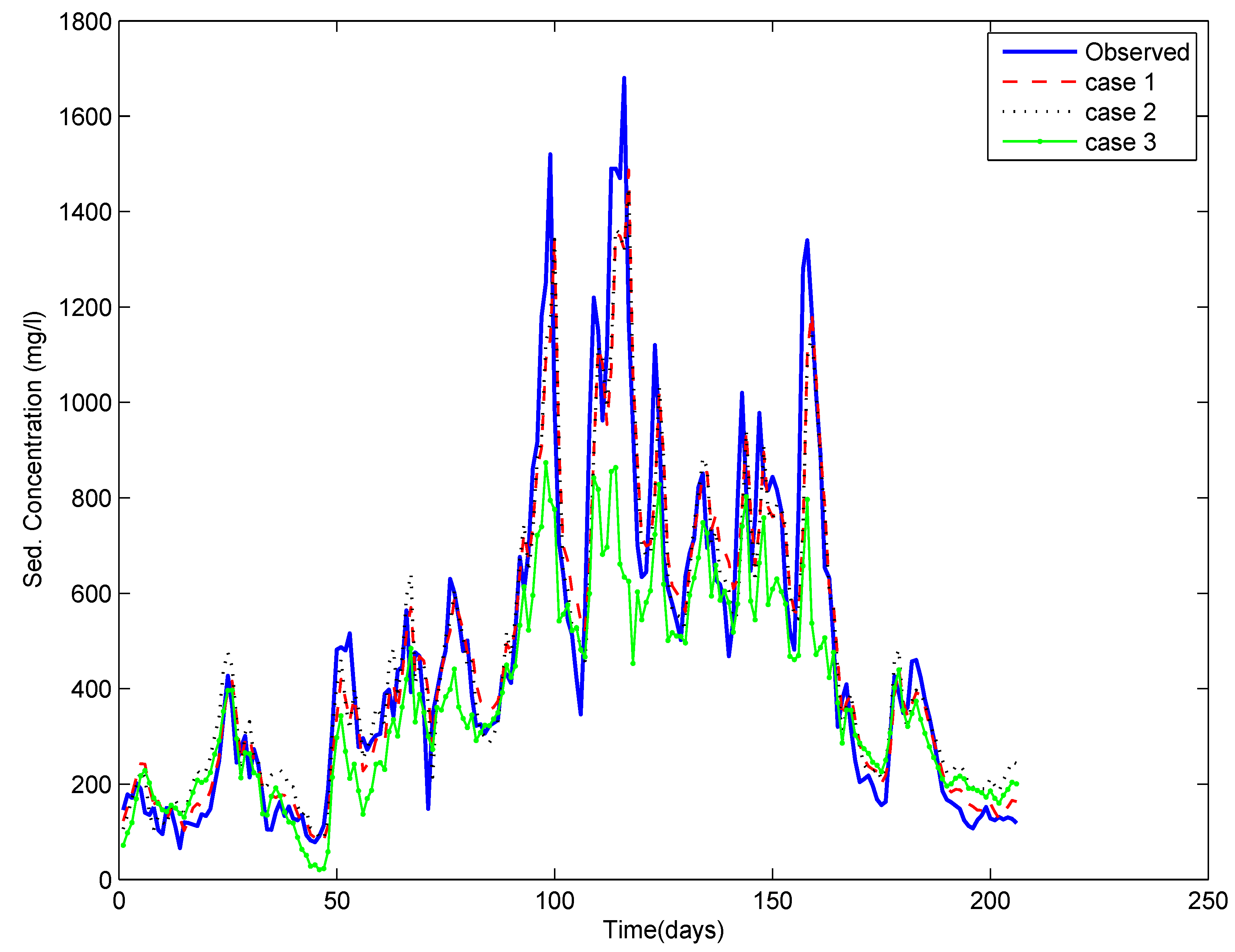
Figure 9. Convex hull of the training and testing set.
Figure 9. Convex hull of the training and testing gear up.
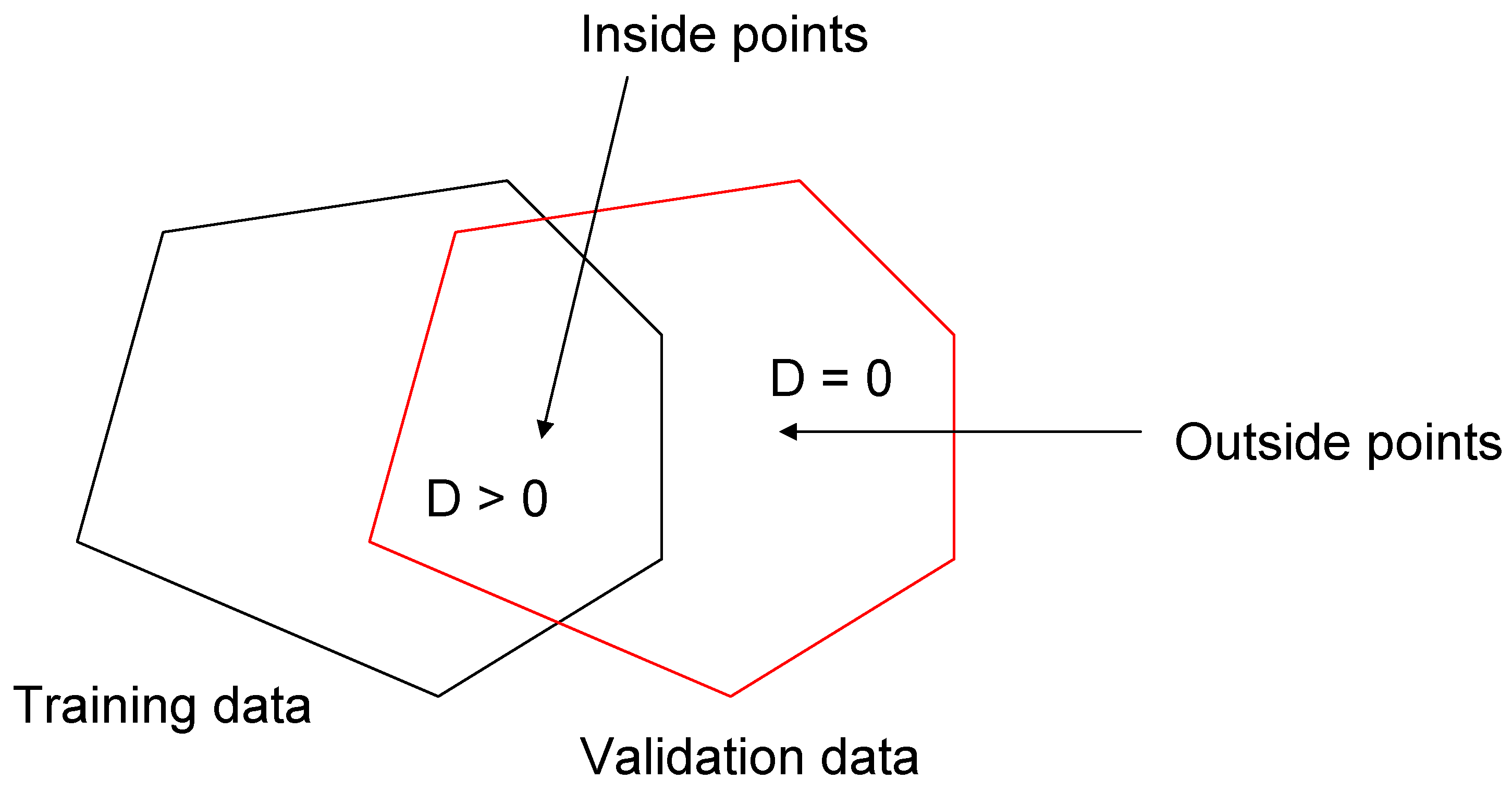
Figure 10. Residuals of the observed and computed discharge at each testing menses for the Chester site.
Effigy 10. Residuals of the observed and computed discharge at each testing period for the Chester site.
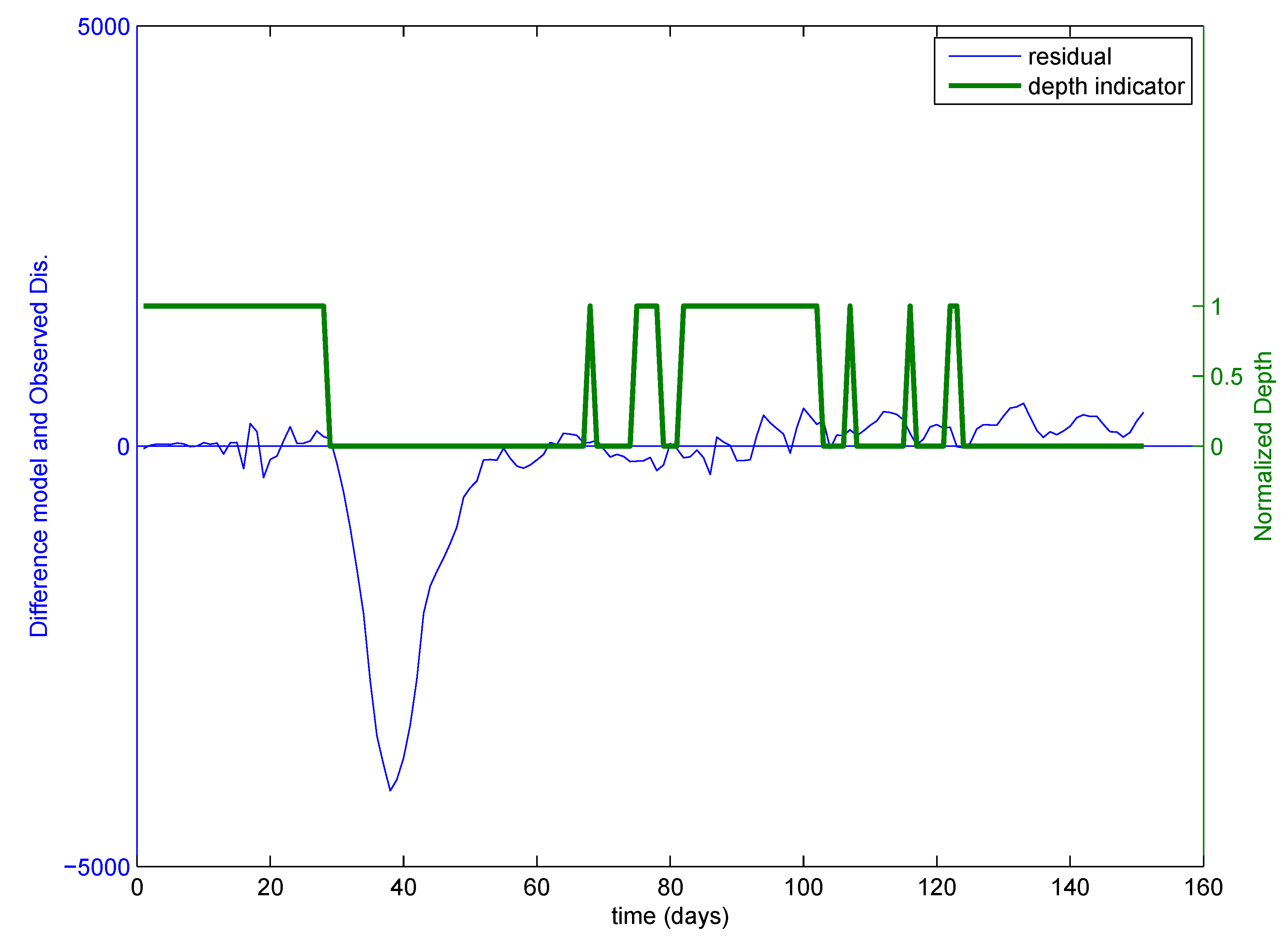
Figure 11. Residuals of the observed and computed sediment concentration at each testing period for the Chester site.
Effigy eleven. Residuals of the observed and computed sediment concentration at each testing period for the Chester site.

The major limitation of the proposed method is the increase in pre-processing time of the data to select the information-rich information. However, one should notation that we are using much less data (near half to one third) to achieve the same result compared to using the whole information gear up. Hence, in specific cases, for example, where we have missing serial, we can achieve reasonable results.
Training of any neural network is considered to be successful if the trained network works well on the testing information set up. The analysis of results and the give-and-take presented above clearly evidence that the ANN trained on critical events has performed every bit well for the tested data set. A model trained using a detail data set is likely to perform well on a test information set if both of the information sets are representative of the system and accept like features. A question arises as how to estimate whether these data sets are similar or non.
To exam this, we did split sampling and divided the data into ii sets, namely training and testing. We located the critical events every bit mentioned in a higher place, and the ANN was trained on the training data set. We validated the trained ANN on the testing set up and calculated the depth of each data point of the testing set in the convex hull of the training set. Thus, we can locate which points of the testing set are in the convex hull of the grooming set up. This practically means how similar the testing set with respect to the training set is. In a written report, Bárdossy and Singh [84] accept used a similar concept in the pick of an appropriate explaining variables for regionalization. Singh et al. [31] used a similar concept and developed the differentiating interpolation and extrapolation (Die) algorithm to define predictive uncertainty. For visual appraisal of the concept, delight refer to Effigy 9. The space where the depth of whatever time step of testing information with respect to the convex hull of the training data is greater than naught ways that the information have very similar properties as the grooming set, and 1 tin can await less residuals and practiced performance. Figure 10 shows the residuals in the model and the observed discharge. In this figure, calculated depth is normalized and plotted along with the remainder to indicate a depth equal to zero or college for each time stride with respect to the training data fix. It can be appreciated from this figure that in the period where depth is nil, the residuum is very high, and in the menses where the depth is higher, the residual is lower. Like results tin can be seen in the case of sediment data, as shown in Figure xi. This shows that the points that are within the convex hull of the training set are the points where we can await depression errors. Practically, it shows that testing points that are in the convex hull of a preparation set are similar to the training set. Hence, one can predict or approximate the functioning of the model a priori by looking at the geometry of the grooming and testing information.
5. Summary and Conclusions
Data from two gauging sites was used to compare the performance of ANN trained on the whole information fix and merely the data from disquisitional events. Selection of information for critical events was washed by ii methods, using the depth part (Ice algorithm) and using random selection. Inter-comparing of the functioning of the ANNs trained using the consummate data sets and the pruned data sets shows that the ANN trained using the data from critical events, i.east., information-rich information, gave similar results as the ANN trained using the complete data set. However, if the data gear up is pruned randomly, the functioning of the ANN degrades significantly. Thus, the choice of events by the depth office by following the method described by [26,27] is not only useful for a conceptual and a physically-based model (as shown past previous studies [26,27,29,30]), merely also for data-driven models. This strategy can result in substantial savings in time and endeavor in the preparation of models based on data-driven approaches, such as ANNs. For any DDMs, training data should have all possible events, which tin describe the process well, irrespective of the length of the data set. There is always swell endeavour and expertise needed to select the proper data fix for the preparation. Therein lies the merit of the Water ice algorithm, which automatically selects all of the possible combinations of events for training. In this study, the well-known back propagation algorithm for preparation neural networks was used, simply the methodology can be used for other kinds of ANNs, such as radial basis function neural networks or support vector machines. This is due to the fact that the option of information-rich data does non depend on the kind of the data-driven models being used. The concept of the newspaper tin exist used to predict the performance of the model a priori by looking at the geometry of the training and testing data. This in turn can be use to define the predictive uncertainty, as given past Singh et al. [31]. A possible criticism of the use of information-rich data could be that it may not result in substantial savings of time, since some time and endeavour will be spent in the identification of critical events. Annotation, nonetheless, that many runs of the ANN model have to be made in the typical case to determine the number of neurons in the hidden layer, etc. Moreover, it is felt that the chances of over fitting are less when data from information-rich events are used for training. There can be many unimportant input variables that may non contribute to the output. Hence, a limitation of the present study is that information technology does not make whatever choice of of import inputs. The results of the present report may be further improved if a proper choice of input variables is made. The authors' side by side piece of work is in the same direction. The suggested methodology can be extended for the selection of input serial among a large number of available input serial. This may reduce the risk of feeding unnecessary or unimportant input series for training. Furthermore, the concept of this paper may be very useful for training data-driven models where the training time serial is incomplete. However, further research is required to complete these task.
Acknowledgments The piece of work described in this paper was supported by a scholarship program initiated past the German language Federal Ministry of Education and Research (BMBF) under the programme of the International Postgraduate Studies in Water Technologies (IPSWaT) for the beginning author. Its contents are solely the responsibility of the authors and exercise not necessarily represent the official position or policy of the High german Federal Ministry of Education and Research and the other organizations to which other authors vest. The authors would like to thank Xuanxuan Guan (editor) and two anonymous reviewers for many useful and constructive suggestions.
Author Contributions
All of the authors take made an equal contribution to this research.
Conflicts of Interest
The authors declare no conflict of involvement.
References
- Maier, H.R.; Great, G.C. Neural networks for the prediction and forecasting of water resource variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, xv, 101–124. [Google Scholar] [CrossRef]
- Bowden, G.J.; Maier, H.R.; Dandy, G.C. Optimal division of information for neural network models in water resources applications. H2o Resour. Res. 2002, 38, 1010. [Google Scholar] [CrossRef]
- Anctil, F.; Perrin, C.; Andréassian, V. Impact of the length of observed records on the performance of ANN and of conceptual parsimonious rainfall-runoff forecasting models. Environm. Model. Softw. 2004, 19, 357–368. [Google Scholar] [CrossRef]
- Bowden, Chiliad.J.; Nifty, G.C.; Maier, H.R. Input decision for neural network models in h2o resources applications. Office ane—Background and methodology. J. Hydrol. 2005, 301, 75–92. [Google Scholar] [CrossRef]
- Leahy, P.; Kiely, Thou.; Corcoran, G. Structural optimisation and input selection of an artificial neural network for river level prediction. J. Hydrol. 2008, 355, 192–201. [Google Scholar] [CrossRef]
- Nawi, N.M.; Atomi, Due west.H.; Rehman, K. The outcome of data pre-processing on optimized training of artificial neural networks. Procedia Technol. 2013, 11, 32–39. [Google Scholar] [CrossRef]
- Marinković, Z.; Marković, 5. Preparation data pre-processing for bias-dependent neural models of microwave transistor handful parameters. Sci. Publ. Country Univ. NOVI Pazar Ser. A Appl. Math. Inform. Mech. 2010, 2, 21–28. [Google Scholar]
- Gaweda, A.E.; Zurada, J.M.; Setiono, R. Input selection in information-driven fuzzy modeling. In Proceedings of the 10th IEEE International Conference of Fuzzy Systems (FUZZ-IEEE), Melbourne, VIC, Australia, 2–5 December 2001; Volume one, pp. 2–v.
- May, R.J.; Maier, H.R.; Neat, 1000.C.; Fernando, T.M.Yard. Non-linear variable selection for artificial neural networks using partial mutual information. Environ. Model. Softw. 2008, 23, 1312–1326. [Google Scholar] [CrossRef]
- Fernando, T.M.K.G.; Maier, H.R.; Great, Thou.C. Selection of input variables for information-driven models: An average shifted histogram partial mutual information computer approach. J. Hydrol. 2009, 367, 165–176. [Google Scholar] [CrossRef]
- Jain, A.; Maier, H.R.; Keen, G.C.; Sudheer, M.P. Rainfall-runoff modeling using neural network: Country-of-art and future research needs. ISH J. Hydraul. Eng. 2009, 15, 52–74. [Google Scholar] [CrossRef]
- Abrahart, R.J.; Anctil, F.; Coulibaly, P.; Dawson, C.Due west.; Mount, Due north.J.; Run into, L.M.; Shamseldin, A.Y.; Solomatine, D.P.; Toth, E.; Wilby, R.Fifty. Two decades of anarchy? Emerging themes and outstanding challenges for neural network river forecasting. Progr. Phys. Geogr. 2012, 36, 480–513. [Google Scholar] [CrossRef]
- Cigizoglu, H.; Kisi, O. Menstruum prediction past three back propagation techniques using thousand-fold partitioning of neural network preparation data. Nordic Hydrol. 2005, 36, 49–64. [Google Scholar]
- Wagener, T.; McIntyre, N.; Lees, Thou.J.; Wheater, H.Southward.; Gupta, H.Five. Towards reduced uncertainty in conceptual rainfall-runoff modelling: Dynamic identifiability assay. Hydrol. Process. 2003, 17, 455–476. [Google Scholar] [CrossRef]
- Chau, Thousand.; Wu, C.; Li, Y. Comparison of several flood forecasting models in Yangtze River. J. Hydrol. Eng. 2005, ten, 485–491. [Google Scholar] [CrossRef]
- Chau, K.W.; Muttil, N. Data mining and multivariate statistical analysis for ecological system in coastal waters. J. Hydroinforma. 2007, ix, 305–317. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W.; Li, Y.S. Methods to amend neural network performance in daily flows prediction. J. Hydrol. 2009, 372, 80–93. [Google Scholar] [CrossRef]
- Wu, C.Fifty.; Chau, One thousand.W.; Li, Y.S. Predicting monthly streamflow using information-driven models coupled with data-preprocessing techniques. Water Resour. Res. 2009, 45, W08432. [Google Scholar] [CrossRef]
- Wu, C.Fifty.; Chau, Chiliad.Due west.; Fan, C. Prediction of rainfall time series using modular artificial neural networks coupled with data-preprocessing techniques. J. Hydrol. 2010, 389, 146–167. [Google Scholar] [CrossRef]
- Chen, Due west.; Chau, K. Intelligent manipulation and scale of parameters for hydrological models. Int. J. Environ. Pollut. 2006, 28, 432–447. [Google Scholar] [CrossRef]
- Wu, C.; Chau, K.; Li, Y. River stage prediction based on a distributed support vector regression. J. Hydrol. 2008, 358, 96–111. [Google Scholar] [CrossRef]
- Wang, West.C.; Xu, D.Thousand.; Chau, K.W.; Chen, South. Improved annual rainfall-runoff forecasting using PSO-SVM model based on EEMD. J. Hydroinform. 2013, 15, 1377–1390. [Google Scholar] [CrossRef]
- Jothiprakash, V.; Kote, A.S. Improving the performance of data-driven techniques through information pre-processing for modelling daily reservoir inflow. Hydrol. Sci. J. 2011, 56, 168–186. [Google Scholar] [CrossRef]
- Moody, J.; Darken, C.J. Fast learning in networks of locally-tuned processing units. Neural Comput. 1989, 1, 281–294. [Google Scholar] [CrossRef]
- Famili, F.; Shen, W.M.; Weber, R.; Simoudis, E. Data pre-processing and intelligent data analysis. Int. J. Intell. Information Anal. 1997, i, 3–23. [Google Scholar] [CrossRef]
- Singh, Due south.Thou.; Bárdossy, A. Identification of critical time periods for the efficient calibration of hydrological models. Geophys. Res. Abstr. 2009, 11, EGU2009-5748. [Google Scholar]
- Singh, South.K.; Bárdossy, A. Calibration of hydrological models on hydrologically unusual events. Adv. Water Resour. 2012, 38, 81–91. [Google Scholar] [CrossRef]
- Tukey, J. Mathematics and Picturing Data. In Proceedings of the 1974 International 17 Congress of Mathematics, Vancouver, BC, Canada, 21–29 August 1975; Volume 2, pp. 523–531.
- Singh, S.G.; Liang, J.; Bárdossy, A. Improving the calibration strategy of the physically-based model WaSiM-ETH using critical events. Hydrol. Sci. J. 2012, 57, 1487–1505. [Google Scholar] [CrossRef]
- Bárdossy, A.; Singh, S.One thousand. Robust interpretation of hydrological model parameters. Hydrol. Earth Syst. Sci. 2008, 12, 1273–1283. [Google Scholar] [CrossRef]
- Singh, S.1000.; McMillan, H.; Bárdossy, A. Use of the information depth function to differentiate between instance of interpolation and extrapolation in hydrological model prediction. J. Hydrol. 2013, 477, 213–228. [Google Scholar] [CrossRef]
- Gupta, V.K.; Sorooshian, S. The relationship betwixt data and the precision of parameter estimates of hydrologic models. J. Hydrol. 1985, 81, 57–77. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Struyf, A. Computing location depth and regression depth in higher dimensions. Stat. Comput. 1998, 8, 193–203. [Google Scholar] [CrossRef]
- Liu, R.Y.; Parelius, J.K.; Singh, K. Multivariate analysis by information depth: Descriptive statistics, graphics and inference. Ann. Stat. 1999, 27, 783–858. [Google Scholar]
- Zuo, Y.; Serfling, R. Full general notions of statistical depth function. Ann. Stat. 2000, 28, 461–482. [Google Scholar] [CrossRef]
- Chebana, F.; Ouarda, T.B.Thou.J. Depth and homogeneity in regional flood frequency analysis. Water Resour. Res. 2008. [Google Scholar] [CrossRef]
- Dutta, S.; Ghosh, A.K.; Chaudhuri, P. Some intriguing properties of Tukey'due south half-space depth. Bernoulli 2011, 17, 1420–1434. [Google Scholar] [CrossRef]
- ASCE Task Committee on Application of Bogus Neural Networks in Hydrology. Artificial neural networks in hydrology, I: Preliminary concepts. J. Hydrol. Eng. 2000, v, 115–123. [Google Scholar] [CrossRef]
- Smith, J.; Eli, R.North. Neural network models of rainfall-runoff process. J. Water Resour. Programme. Manag. 1995, 121, 499–508. [Google Scholar] [CrossRef]
- ASCE Task Committee on Application of Artificial Neural Networks in Hydrology. Artificial neural networks in hydrology, Two: Hydrological applications. J. Hydrol. Eng. 2000, 5, 124–137. [Google Scholar] [CrossRef]
- Maier, H.; Jain, A.; Keen, G.; Sudheer, G.P. Methods used for the evolution of neural networks for the prediction of water resources variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Govindaraju, R.South.; Rao, A. Artificial Neural Networks in Hydrology; Kluwer Bookish Publishers: Dordrecht, Kingdom of the netherlands, 2000. [Google Scholar]
- Cigizoglu, H.Thou. Estimation, forecasting and extrapolation of river flows by artificial neural networks. Hydrol. Sci. J. 2003, 48, 349–361. [Google Scholar] [CrossRef]
- Wilby, R.50.; Abrahart, R.J.; Dawson, C.Due west. Detection of conceptual model rainfall-runoff processes inside an artificial neural network. Hydrol. Sci. J. 2003, 48, 163–181. [Google Scholar] [CrossRef]
- Lin, M.F.; Chen, 50.H. A non-linear rainfall-runoff model using radial footing function network. J. Hydrol. 2004, 289, ane–viii. [Google Scholar] [CrossRef]
- Imrie, C.East.; Durucan, S.; Korre, A. River period prediction using artificial neural networks: Generalization beyond the scale range. J. Hydrol. 2000, 233, 138–153. [Google Scholar] [CrossRef]
- Lekkas, D.F.; Imrie, C.E.; Lees, M.J. Improved non-linear transfer function and neural network methods of menses routing for real-time forecasting. J. Hydroinforma. 2001, 3, 153–164. [Google Scholar]
- Shrestha, R.R.; Theobald, S.; Nestmann, F. Simulation of flood period in a river arrangement using artificial neural networks. Hydrol. Earth Syst. Sci. 2005, 9, 313–321. [Google Scholar] [CrossRef]
- Campolo, Yard.; Soldati, A.; Andreussi, P. Artificial neural network arroyo to overflowing forecasting in the River Arno. Hydrol. Sci. J. 2003, 48, 381–398. [Google Scholar] [CrossRef]
- Jain, S.Grand.; Das, A.; Srivastava, D.K. Awarding of ANN for reservoir arrival prediction and operation. J. H2o Resour. Program. Manag. ASCE 1999, 125, 263–271. [Google Scholar] [CrossRef]
- Jain, South.K.; Singh, V.P.; van Genuchten, Thou. Awarding of ANN for reservoir inflow prediction and operation. J. Water Resour. Programme. Manag. ASCE 2004, 9, 415–420. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Lobbrecht, A.H.; Solomatine, D.P. Neural networks and reinforcement learning in control of water systems. J. Water Resour. Plan. Manag. ASCE 2003, 129, 458–465. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, Thousand.Due west.; Sethi, R. Artificial neural network simulation of hourly groundwater levels in a coastal aquifer organization of the Venice Lagoon. Eng. Appl. Artif. Intell. 2012, 25, 1670–1676. [Google Scholar] [CrossRef]
- Cheng, C.; Chau, K.; Sun, Y.; Lin, J. Long-term prediction of discharges in Manwan reservoir using artificial neural network models. Lect. Notes Comput. Sci. 2005, 3498, 1040–1045. [Google Scholar]
- Zealand, C.Thousand.; Burn, D.H.; Simonovic, S.P. Brusk term streamflow forecasting using artificial neural networks. J. Hydrol. 1999, 214, 32–48. [Google Scholar] [CrossRef]
- Tokar, A.S.; Johnson, P.A. Rainfall-runoff modelling using artificial neural networks. J. Hydrol. Eng. 1999, 4, 232–239. [Google Scholar] [CrossRef]
- Cigizoglu, H.Thousand. Estimation and forecasting of daily suspended sediment data by multi layer perceptrons. Adv. Water Resour. 2004, 27, 185–195. [Google Scholar] [CrossRef]
- Sudheer, K.P.; Jain, A. Explaining the internal behaviour of artificial neural network river flow models. Hydrol. Procedure. 2004, 18, 833–844. [Google Scholar] [CrossRef]
- Kumar, A.R.S.; Sudheer, Chiliad.P.; Jain, South.M. Rainfall-runoff modeling using artificial neural networks: Comparison of network types. Hydrol. Process. 2005, xix, 1277–1291. [Google Scholar] [CrossRef]
- Cigizoglu, H.K.; Kisi, O. Flow prediction by 3 back propagation techniques using k-fold partitioning of neural network grooming information. Nordic Hydrol. 2005, 361, 1–16. [Google Scholar]
- Cigizoglu, H.M.; Kisi, O. Methods to improve the neural network performance in suspended sediment interpretation. J. Hydrol. 2006, 317, 221–238. [Google Scholar] [CrossRef]
- Cigizoglu, H.Grand.; Alp, Yard. Generalized regression neural network in modelling river sediment yield. Adv. Eng. Softw. 2006, 372, 63–68. [Google Scholar] [CrossRef]
- Lin, J.; Cheng, C.T.; Chau, K.W. Using support vector machines for long-term discharge prediction. Hydrol. Sci. J. 2006, 51, 599–612. [Google Scholar] [CrossRef]
- Alp, M.; Cigizoglu, H.K. Suspended sediment estimation by feed forward dorsum propagation method using hydro meteorological information. Environ. Model. Softw. 2007, 22, 2–thirteen. [Google Scholar] [CrossRef]
- Solomatine, D.; Ostfeld, A. Data-driven modelling: Some past experiences and new approaches. J. Hydroinform. 2008, ten, 3–22. [Google Scholar] [CrossRef]
- Shamseldin, A. Artificial neural network model for river flow forecasting in a developing country. J. Hydroinform. 2010, 12, 22–35. [Google Scholar] [CrossRef]
- Kumar, Grand.; Raghuwanshi, North.S.; Singh, R.; Wallender, Due west.W.; Pruitt, W.O. Estimating evapotranspiration using artificial neural network. J. Irrig. Drain. Eng. ASCE 2002, 128, 224–233. [Google Scholar] [CrossRef]
- Sudheer, K.P.; Gosain, A.K.; Rangan, D.M.; Saheb, Southward.K. Modeling evaporation using bogus neural network algorithm. Hydrol. Process. 2002, 16, 3189–3202. [Google Scholar] [CrossRef]
- Keskin, M.E.; Terzi, O. Artificial Neural Network models of daily pan evaporation. J. Hydrol. Eng. 2006, xi, 65–70. [Google Scholar] [CrossRef]
- Sudheer, K.P.; Jain, South.Chiliad. Radial basis part neural networks for modelling rating curves. J. Hydrol. Eng. 2003, 8, 161–164. [Google Scholar] [CrossRef]
- Trajkovic, South.; Todorovic, B.; Stankovic, M. Forecasting reference evapotranspiration by artificial neural networks. J. Irrig. Drain. Eng. 2003, 129, 454–457. [Google Scholar] [CrossRef]
- Kisi, O. Evapotranspiration modeling from climatic information using a neural calculating technique. Hydrol. Process. 2007, 21, 1925–1934. [Google Scholar] [CrossRef]
- Kisi, O. Generalized regression neural networks for evapotranspiration modeling. J. Hydrol. Sci. 2006, 51, 1092–1105. [Google Scholar] [CrossRef]
- Kisi, O.; Öztürk, O. Adaptive neurofuzzy computing technique for evapotranspiration estimation. J. Irrig. Drain. Eng. 2007, 133, 368. [Google Scholar] [CrossRef]
- Jain, Southward.K.; Nayak, P.C.; Sudheer, K.P. Models for estimating evapotranspiration using artificial neural networks, and their concrete estimation. Hydrol. Process. 2008, 22, 2225–2234. [Google Scholar] [CrossRef]
- Muttil, N.; Chau, K.Westward. Neural network and genetic programming for modelling littoral algal blooms. Int. J. Environ. Pollut. 2006, 28, 223–238. [Google Scholar] [CrossRef]
- Zhang, Q.; Stanley, S.J. Forecasting raw-h2o quality parameters for the N Saskatchewan River by neural network modeling. H2o Res. 1997, 31, 2340–2350. [Google Scholar] [CrossRef]
- Palani, S.; Liong, S.Y.; Tkalich, P. An ANN application for water quality forecasting. Marine Pollut. Balderdash. 2008, 56, 1586–1597. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.P.; Basant, A.; Malik, A.; Jain, G. Artificial neural network modeling of the river water quality—A case study. Ecol. Model. 2009, 220, 888–895. [Google Scholar] [CrossRef]
- Jain, S.One thousand. Development of integrated sediment rating curves using ANNS. J. Hydraul. Eng. 2001, 127, 30–37. [Google Scholar] [CrossRef]
- Porterfield, G. Ciphering of fluvial-sediment discharge. In Techniques of H2o-Resource Investigations of the Us Geological Survey; US Government Printing Office: Washington, DC, United states of america, 1972; Chapter C3; pp. 1–66. [Google Scholar]
- USGS Sediment Data Portal. Available online: http://co.water.usgs.gov/sediment/introduction.html (accessed on 30 September 2009).
- Jain, S.K.; Chalisgaonkar, D. Setting up stage-discharge relations using ANN. J. Hydrol. Eng. 2000, 5, 428–433. [Google Scholar] [CrossRef]
- Bárdossy, A.; Singh, S.K. Regionalization of hydrological model parameters using data depth. Hydrol. Res. 2011, 42, 356–371. [Google Scholar] [CrossRef]
© 2014 past the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and atmospheric condition of the Creative Eatables Attribution license (http://creativecommons.org/licenses/by/3.0/).
murraypritioneatch.blogspot.com
Source: https://www.mdpi.com/2306-5338/1/1/40/htm
0 Response to "Rainfall Runoff Modelling Using Neural Networks Stateoftheart and Future Research Needs"
Post a Comment